การคำนวณความแปรปรวนของ Excel: คำแนะนำพร้อมตัวอย่าง
ความแปรปรวนเป็นหน่วยวัดทางสถิติที่บอกเราว่าชุดตัวเลขมีการกระจายออกไปมากน้อยเพียงใด เป็นแนวคิดที่สำคัญในด้านการเงิน วิทยาศาสตร์ และสาขาอื่นๆ อีกมากมาย ซึ่งช่วยให้เราเข้าใจความแปรปรวนหรือการกระจายตัวภายในชุดข้อมูลของเรา Excel มอบวิธีที่ตรงไปตรงมาในการคำนวณความแปรปรวน ทำให้ทั้งผู้เริ่มต้นและผู้ใช้ขั้นสูงสามารถเข้าถึงได้ ในบทความนี้ เราจะสำรวจวิธีการทำเช่นนี้พร้อมตัวอย่างที่ชัดเจน
ความแปรปรวนคืออะไร?
ความรู้เบื้องต้นเกี่ยวกับฟังก์ชันผลต่างของ Excel
วิธีการคำนวณความแปรปรวนใน Excel?
- VAR.S กับ VAR.P – คำนวณความแปรปรวนจากตัวอย่างหรือประชากร
- VAR.S เทียบกับ VARA – คำนวณความแปรปรวนรวมถึงหรือไม่รวมข้อความและข้อความเชิงตรรกะ
ความแปรปรวนเทียบกับส่วนเบี่ยงเบนมาตรฐาน
ความแปรปรวนคืออะไร?
ความแปรปรวนเป็นคำศัพท์ทางสถิติที่อธิบายขอบเขตที่ตัวเลขในชุดข้อมูลแตกต่างจากค่าเฉลี่ยหรือค่าเฉลี่ยของตัวเลข โดยพื้นฐานแล้ว จะวัดว่าตัวเลขกระจายตัวอย่างไร ประเด็นสำคัญในการทำความเข้าใจความแปรปรวนคือการรับรู้ว่าความแปรปรวนนั้นวัดปริมาณระดับของการแปรผันหรือการกระจายตัวภายในชุดของค่า ความแปรปรวนสูงบ่งชี้ว่าตัวเลขมีการกระจายออกไป ความแปรปรวนต่ำบ่งบอกว่าพวกมันอยู่รวมกันเป็นกลุ่มอย่างใกล้ชิดกับค่าเฉลี่ย
ตัวอย่างง่ายๆ เพื่อแสดงให้เห็นความแปรปรวน:
สถานการณ์: พิจารณาชั้นเรียนที่มีนักเรียน 100 คนและคะแนนของพวกเขาในการทดสอบคณิตศาสตร์เต็ม 90 คะแนนคือ 92, 88, 91, 89 และ XNUMX
คำนวณค่าเฉลี่ย: ขั้นแรกให้หาคะแนนเฉลี่ย (ค่าเฉลี่ย) ค่าเฉลี่ยคือ
คำนวณความแปรปรวน: จากนั้นเราคำนวณความแปรปรวน ซึ่งเกี่ยวข้องกับการลบค่าเฉลี่ยออกจากแต่ละคะแนน ยกกำลังสองผลลัพธ์ แล้วจึงหาค่าเฉลี่ยผลต่างกำลังสองเหล่านี้
= [0 + 4 + 4 + 1 + 1] / 5
= 10/5
= 2
แผนภูมิแสดงการแพร่กระจายของคะแนน:
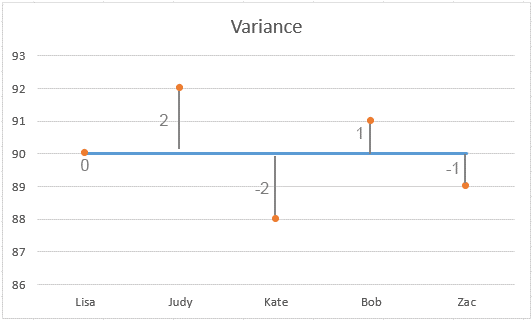
การทำความเข้าใจผลลัพธ์:
ความแปรปรวนต่ำ: ในตัวอย่างนี้ ความแปรปรวนคือ 2 ซึ่งค่อนข้างต่ำ ซึ่งบ่งชี้ว่าคะแนนส่วนใหญ่ใกล้เคียงกับค่าเฉลี่ย (90) ยิ่งความแปรปรวนต่ำ ตัวเลขแต่ละตัวในชุดก็จะยิ่งเข้าใกล้ค่าเฉลี่ยมากขึ้นเท่านั้น
ความแปรปรวนเป็นศูนย์: ถ้านักเรียนทุกคนได้คะแนน 90 พอดี ความแปรปรวนจะเป็น 0 ซึ่งบ่งชี้ว่าไม่มีความแปรปรวนเลย แต่ละคะแนนจะเท่ากัน
ความแปรปรวนสูง: ในทางกลับกัน ความแปรปรวนที่สูงกว่าจะบ่งชี้ว่าคะแนนมีการกระจายออกจากค่าเฉลี่ยมากกว่า ซึ่งแสดงความแปรปรวนในผลการเรียนของนักเรียนมากขึ้น
โดยสรุป ความแปรปรวนให้ค่าตัวเลขที่ช่วยบอกจำนวนว่าคะแนน (หรือชุดตัวเลขใดๆ) เบี่ยงเบนไปจากค่าเฉลี่ยมากน้อยเพียงใด โดยให้ข้อมูลเชิงลึกเกี่ยวกับความสอดคล้องหรือความแปรปรวนของข้อมูล
ความรู้เบื้องต้นเกี่ยวกับฟังก์ชันผลต่างของ Excel
Excel มีฟังก์ชันหลายอย่างในการคำนวณความแปรปรวน ซึ่งแต่ละฟังก์ชันได้รับการออกแบบมาสำหรับสถานการณ์ข้อมูลที่แตกต่างกัน
การทำความเข้าใจฟังก์ชันเหล่านี้เป็นสิ่งสำคัญสำหรับการวิเคราะห์ทางสถิติที่แม่นยำ
วาร์.เอส (ความแปรปรวนตัวอย่าง รวมเฉพาะตัวเลข):
- คำนวณความแปรปรวนตามกลุ่มตัวอย่างประชากร
- ใช้ดีที่สุดเมื่อวิเคราะห์ชุดย่อยของข้อมูลเพื่ออนุมานเกี่ยวกับข้อมูลทั้งหมด
วีเออาร์พี (ความแปรปรวนของประชากร รวมเฉพาะตัวเลข):
- คำนวณความแปรปรวนของประชากรทั้งหมด
- เหมาะสำหรับเมื่อคุณมีข้อมูลครบถ้วน ไม่ใช่เพียงตัวอย่าง
วรา (ความแปรปรวนตัวอย่าง รวมถึงข้อความและตรรกะ):
- คล้ายกับ VAR.S แต่รวมข้อความและค่าตรรกะในการคำนวณ (ข้อความจะถือเป็น 0, TRUE เป็น 1, FALSE เป็น 0)
- มีประโยชน์เมื่อชุดข้อมูลของคุณมีประเภทผสม (ตัวเลข ข้อความ และค่าตรรกะ)
วาร์ป (ความแปรปรวนของประชากร รวมถึงข้อความและตรรกะ):
- เวอร์ชันความแปรปรวนประชากรของ VARA
- รวมข้อมูลทุกประเภทในการคำนวณผลต่างสำหรับประชากรทั้งหมด
VAR (ความแปรปรวนตัวอย่างแบบเดิม):
- VAR.S เวอร์ชันเก่า ซึ่งใช้เป็นหลักใน Excel 2007 และเวอร์ชันก่อนหน้า
- ขอแนะนำให้ใช้ VAR.S ในเวอร์ชันที่ใหม่กว่าเพื่อความสม่ำเสมอและความชัดเจน
วีอาร์พี (ความแปรปรวนของประชากรแบบเดิม):
- VAR.P. เวอร์ชันเก่า
- เช่นเดียวกับ VAR ขอแนะนำให้ใช้ VAR.P ใน Excel เวอร์ชันใหม่กว่า
ความแตกต่างและการเปรียบเทียบ:
- ตัวอย่างกับประชากร: VAR.S และ VARA มีไว้สำหรับตัวอย่าง ในขณะที่ VAR.P และ VARPA มีไว้สำหรับประชากรทั้งหมด
- การพิจารณาประเภทข้อมูล: VARA และ VARPA รวมข้อความและค่าตรรกะในการคำนวณ ซึ่งแตกต่างจาก VAR.S และ VAR.P
- ฟังก์ชันรุ่นเก่ากับฟังก์ชันสมัยใหม่: VAR และ VARP เป็นฟังก์ชันเก่าและสามารถแทนที่ได้ด้วย VAR.S และ VAR.P เพื่อให้เข้ากันได้ดียิ่งขึ้นกับ Excel เวอร์ชันปัจจุบัน
ตารางเปรียบเทียบ:
| ฟังก์ชัน | พิจารณาประเภทข้อมูลแล้ว | ประชากรหรือกลุ่มตัวอย่าง | ใช้กรณี |
| วาร์.เอส | ตัวเลขเท่านั้น | ตัวอย่าง | ความแปรปรวนตัวอย่างสำหรับข้อมูลตัวเลข |
| วีเออาร์พี | ตัวเลขเท่านั้น | ประชากร | ความแปรปรวนของประชากรสำหรับตัวเลข |
| วรา | ตัวเลข ข้อความ ตรรกะ | ตัวอย่าง | ความแปรปรวนตัวอย่างสำหรับข้อมูลแบบผสม |
| วาร์ป | ตัวเลข ข้อความ ตรรกะ | ประชากร | ความแปรปรวนของประชากรสำหรับข้อมูลแบบผสม |
| VAR | ตัวเลขเท่านั้น | ตัวอย่าง | ฟังก์ชันดั้งเดิมสำหรับความแปรปรวนตัวอย่าง |
| วีอาร์พี | ตัวเลขเท่านั้น | ประชากร | ฟังก์ชั่นดั้งเดิมสำหรับความนิยม |
วิธีการคำนวณความแปรปรวนใน Excel?
ในส่วนนี้ เราจะให้สองตัวอย่างเพื่อสาธิตวิธีการคำนวณผลต่างใน Excel และอธิบายความแตกต่างระหว่างฟังก์ชันผลต่างต่างๆ ด้วยเหตุนี้ คุณจะเห็นว่าฟังก์ชันความแปรปรวนที่แตกต่างกันให้ผลลัพธ์ที่แตกต่างกันโดยสิ้นเชิงสำหรับข้อมูลตัวอย่างเดียวกัน
VAR.S กับ VAR.P – คำนวณความแปรปรวนจากตัวอย่างหรือประชากร
สถานการณ์: กำลังคำนวณความแปรปรวนของกลุ่มตัวอย่างเล็กๆ ของประชากรเทียบกับประชากรทั้งหมด
ตัวอย่าง: คำนวณความแปรปรวนของค่าในคอลัมน์ A2:A12
สูตร: เลือกเซลล์ว่างแล้วพิมพ์สูตรใดสูตรหนึ่งด้านล่างตามที่คุณต้องการ จากนั้นกด Enter กุญแจ
-
รับความแปรปรวนสำหรับตัวอย่างของชุดข้อมูลขนาดใหญ่ (สมมติว่าค่าใน A2:A12 เป็นส่วนหนึ่งของชุดข้อมูลขนาดใหญ่)
=VAR.S(A2:A12)
-
รับค่าความแปรปรวนสำหรับประชากรทั้งหมด (สมมติว่าค่าใน A2:A12 เป็นชุดข้อมูลทั้งหมด)
=VAR.P(A2:A12)
อย่างที่คุณเห็น ค่าเดียวกันแต่ใช้ฟังก์ชันความแปรปรวนต่างกันจะได้ผลลัพธ์ที่แตกต่างกัน
เหตุใดผลลัพธ์ของ VAR.S และ VAR.P จึงแตกต่างกัน?
- วาร์.เอส: ฟังก์ชันนี้ใช้เมื่อชุดข้อมูลของคุณแสดงตัวอย่างจากประชากรจำนวนมาก โดยจะคำนวณความแปรปรวนตามวิธี "n-1" โดยที่ "n" คือจำนวนจุดข้อมูลในตัวอย่าง การใช้ "n-1" แทน "n" เป็นตัวส่วนจะแก้ไขอคติในกลุ่มตัวอย่าง ทำให้เป็นตัวประมาณค่าความแปรปรวนของประชากรที่เป็นกลาง โดยจะให้ค่าประมาณว่าข้อมูลในกลุ่มตัวอย่างแตกต่างกันอย่างไรตามค่าเฉลี่ยของกลุ่มตัวอย่าง
- วีเออาร์พี: ฟังก์ชันนี้ใช้เมื่อชุดข้อมูลของคุณแสดงถึงประชากรทั้งหมด ไม่ใช่แค่ตัวอย่างจากชุดข้อมูลนั้น โดยจะคำนวณความแปรปรวนตามวิธี "n" โดยที่ "n" คือจำนวนจุดข้อมูลในประชากร โดยถือว่าชุดข้อมูลครอบคลุมประชากรทั้งหมด ดังนั้นจึงไม่จำเป็นต้องแก้ไขอคติเหมือนใน VAR.S
- ในการสรุปความแตกต่างที่สำคัญอยู่ที่ตัวส่วนของสูตร VAR.S ใช้ "n-1" เพื่อพิจารณาลักษณะตัวอย่างของข้อมูล ในขณะที่ VAR.P ใช้ "n" สำหรับข้อมูลประชากรที่ไม่มีการสุ่มตัวอย่างที่เกี่ยวข้อง ขึ้นอยู่กับชุดข้อมูลของคุณและไม่ว่าจะเป็นกลุ่มตัวอย่างหรือประชากรเต็ม คุณควรเลือกฟังก์ชันที่เหมาะสมในการคำนวณความแปรปรวน
VAR.S กับ VAR.P – คำนวณความแปรปรวนจากตัวอย่างหรือประชากร
สถานการณ์: ตัดสินใจว่าจะรวมค่าตรรกะและข้อความในการคำนวณผลต่างหรือไม่
ตัวอย่าง: คำนวณความแปรปรวนของค่าในคอลัมน์ A2:A12
สูตร: เลือกเซลล์ว่างแล้วพิมพ์สูตรใดสูตรหนึ่งด้านล่างตามที่คุณต้องการ จากนั้นกด Enter กุญแจ
-
รับค่าความแปรปรวนสำหรับตัวอย่างของชุดข้อมูลขนาดใหญ่โดยไม่สนใจข้อความและค่าตรรกะ
=VAR.S(A2:A12)
-
รับค่าความแปรปรวนสำหรับตัวอย่างของชุดข้อมูลขนาดใหญ่ รวมถึงข้อความและค่าตรรกะ
=VARA(A2:A12)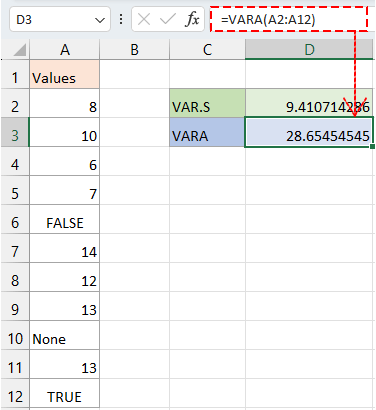
ทำให้การคำนวณวันที่และเวลาบินได้
Kutools สำหรับ Excel's ตัวช่วยวันที่และเวลา เป็นเครื่องมือที่มีประสิทธิภาพอย่างเหลือเชื่อที่ออกแบบมาเพื่อลดความซับซ้อนในการคำนวณวันที่และเวลา ลองดูว่ามันเปลี่ยนประสบการณ์การจัดการข้อมูลของคุณอย่างไร!
ความแปรปรวนเทียบกับส่วนเบี่ยงเบนมาตรฐาน
ความคล้ายคลึงกัน:
-
การวัดการแพร่กระจาย:
ทั้งความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานเป็นการวัดทางสถิติที่ใช้อธิบายการแพร่กระจายหรือการกระจายตัวภายในชุดข้อมูล โดยจะคำนวณว่าตัวเลขแต่ละตัวในชุดเบี่ยงเบนไปจากค่าเฉลี่ย (ค่าเฉลี่ย) มากเพียงใด
-
การวิเคราะห์ข้อมูล:
โดยทั่วไปจะใช้ทั้งสองอย่างในการวิเคราะห์ทางสถิติเพื่อทำความเข้าใจความแปรปรวนของข้อมูล สิ่งเหล่านี้มีความสำคัญในสาขาต่างๆ เช่น การเงิน การวิจัย การควบคุมคุณภาพ และอื่นๆ
-
คำนวณจากค่าเฉลี่ย:
การคำนวณทั้งความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานเริ่มต้นด้วยค่าเฉลี่ยของชุดข้อมูล พวกเขาประเมินความแปรปรวนที่เกี่ยวข้องกับค่ากลางนี้
แตกต่าง:
-
หน่วยวัด:
-
ความแปรปรวน: หน่วยกำลังสองของข้อมูลต้นฉบับ เช่น หากข้อมูลมีหน่วยเป็นเมตร ความแปรปรวนจะมีหน่วยเป็นตารางเมตร
-
ส่วนเบี่ยงเบนมาตรฐาน: หน่วยเดียวกับข้อมูลต้นฉบับ ดำเนินการต่อจากตัวอย่าง หากข้อมูลมีหน่วยเป็นเมตร ส่วนเบี่ยงเบนมาตรฐานก็จะเป็นหน่วยเมตรด้วย
-
-
การตีความ:
-
ความแปรปรวน: ให้ค่าประมาณกำลังสองซึ่งสามารถตีความได้ยาก เนื่องจากไม่ได้มีขนาดเท่ากับข้อมูลต้นฉบับ
-
ส่วนเบี่ยงเบนมาตรฐาน: ตีความได้มากขึ้นเนื่องจากอยู่ในหน่วยเดียวกับข้อมูล โดยจะแสดงระยะทางเฉลี่ยของจุดข้อมูลจากค่าเฉลี่ย
-
-
ความหมายทางคณิตศาสตร์:
-
ความแปรปรวน: ค่าเฉลี่ยของผลต่างกำลังสองจากค่าเฉลี่ย
-
ค่าเบี่ยงเบนมาตรฐาน: รากที่สองของความแปรปรวน
-
-
ความไวต่อค่านิยมสูงสุด:
-
ความแปรปรวน: มีความอ่อนไหวต่อค่าผิดปกติมากกว่าเนื่องจากจะทำให้ความแตกต่างเป็นกำลังสอง
-
ค่าเบี่ยงเบนมาตรฐาน: แม้ว่าจะได้รับผลกระทบจากค่าผิดปกติ แต่ก็มีความไวน้อยกว่าเมื่อเทียบกับความแปรปรวนเนื่องจากรากที่สอง
-
-
การใช้งาน:
-
ผลต่าง:
ใช้เมื่อโฟกัสอยู่ที่ขนาดการกระจายตัวกำลังสอง
มีประโยชน์ในแบบจำลองทางสถิติและการคำนวณที่จำเป็นต้องยกกำลังสองเพื่อทำให้ค่าลบเป็นโมฆะ
มักใช้ในแบบจำลองทางการเงินเพื่อการประเมินความเสี่ยง เนื่องจากเป็นการวัดความผันผวน
-
ส่วนเบี่ยงเบนมาตรฐาน:
ใช้กันทั่วไปในรายงานและแอปพลิเคชันรายวันเนื่องจากมีความสัมพันธ์โดยตรงกับขนาดข้อมูล
จำเป็นในการวิจัยเชิงประจักษ์เพื่อทำความเข้าใจความแปรปรวน
ใช้บ่อยในการควบคุมคุณภาพ รายงานสภาพอากาศ และคะแนนมาตรฐานในการทดสอบ
-
สรุป:
แม้ว่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานจะใช้ในการวัดการแพร่กระจายของชุดข้อมูล แต่การใช้งานจะแตกต่างกันเนื่องจากหน่วยการวัดและการตีความ ค่าเบี่ยงเบนมาตรฐานซึ่งมีความสัมพันธ์โดยตรงกับขนาดของข้อมูล มีแนวโน้มที่จะเป็นมิตรกับผู้ใช้มากกว่า โดยเฉพาะอย่างยิ่งในบริบทที่ใช้งานได้จริงในชีวิตประจำวัน ในทางกลับกัน ความแปรปรวนมักจะเหมาะกับแบบจำลองทางคณิตศาสตร์และสถิติมากกว่า
ภาพรวมและการเปรียบเทียบนี้ควรให้ความเข้าใจที่ชัดเจนว่าเมื่อใดและเพราะเหตุใดจึงควรใช้ฟังก์ชันความแปรปรวนแต่ละรายการใน Excel ช่วยให้วิเคราะห์ข้อมูลได้แม่นยำและมีความหมายมากขึ้น สำหรับกลยุทธ์ Excel ที่เปลี่ยนแปลงเกมได้มากขึ้นซึ่งสามารถยกระดับการจัดการข้อมูลของคุณ สำรวจเพิ่มเติมได้ที่นี่.
เครื่องมือเพิ่มประสิทธิภาพการทำงานในสำนักงานที่ดีที่สุด
Kutools สำหรับ Excel - ช่วยให้คุณโดดเด่นจากฝูงชน
Kutools สำหรับ Excel มีคุณสมบัติมากกว่า 300 รายการ รับรองว่าสิ่งที่คุณต้องการเพียงแค่คลิกเดียว...

แท็บ Office - เปิดใช้งานการอ่านแบบแท็บและการแก้ไขใน Microsoft Office (รวม Excel)
- หนึ่งวินาทีเพื่อสลับไปมาระหว่างเอกสารที่เปิดอยู่มากมาย!
- ลดการคลิกเมาส์หลายร้อยครั้งสำหรับคุณทุกวันบอกลามือเมาส์
- เพิ่มประสิทธิภาพการทำงานของคุณได้ถึง 50% เมื่อดูและแก้ไขเอกสารหลายฉบับ
- นำแท็บที่มีประสิทธิภาพมาสู่ Office (รวมถึง Excel) เช่นเดียวกับ Chrome, Edge และ Firefox

สารบัญ
- ความแปรปรวนคืออะไร?
- ความรู้เบื้องต้นเกี่ยวกับฟังก์ชันผลต่างของ Excel
- วิธีการคำนวณความแปรปรวนใน Excel?
- VAR.S กับ VAR.P – คำนวณความแปรปรวนจากตัวอย่างหรือประชากร
- VAR.S เทียบกับ VARA – คำนวณความแปรปรวนรวมถึงหรือไม่รวมข้อความและข้อความเชิงตรรกะ
- ความแปรปรวนเทียบกับส่วนเบี่ยงเบนมาตรฐาน
- บทความที่เกี่ยวข้อง
- สุดยอดเครื่องมือเพิ่มผลผลิตในสำนักงาน
- ความคิดเห็น